デジタル時代になってから一眼レフのファインダー倍率が小さくなったとよく言われる。もちろんフルサイズならそれほどでもないが、APS-C、ましてやフォーサーズともなるとその小ささは顕著なものとなる。よく「井戸の底を覗くよう」とか「トンネルの向こうの景色」みたいな揶揄をされることがあるが、本当にE-620のファインダーを覗いた後でOM-4Tiのファインダーを覗くと、あまりの大きさにたまげそうになる。ファインダー倍率が小さいと、一般的にはMFでのピント合わせがしづらくなることが最も大きな問題とされている。もっとも現代のカメラはすべてAFが当たり前だから、AF専用と割り切れば実用上問題ないとも言えるのだが、どうしてもピントが合いにくいときやMFレンズを使わざるを得ないときは困ったことになってしまう。
ファインダー倍率はカタログスペック上では0.xx倍という数値で表されるが、その意味は正しく理解されているのだろうか? そしてデジタルカメラのファインダー倍率の表記は実はインチキであることに、どのくらいの人が気づいているのだろうか? 自分も最近までよくわかっていなかったのだが、この辺のことをもう一度整理して考えてみたい。
まず一眼レフカメラの構造を簡単に振り返ってみよう。下の図は一眼レフの光路を概略的に示したものである。
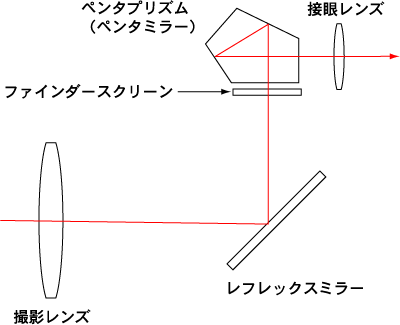
撮影レンズから入った光はまずレフレックスミラーで反射され、ファインダースクリーン上に像を結ぶ。当然、撮影レンズからファインダースクリーンまでの距離は、フィルムあるいは撮像素子までの距離と厳密に等しい。そうでなければピントは合わない。またこの距離が撮影レンズの焦点距離であることは言うまでもない。ただし、ファインダースクリーンに映る像は上下左右が逆であるため、これを正立像に戻すのがペンタプリズムの働きだ。五角形のペンタプリズム内部で3回反射されることによって正立像となり、その後接眼レンズを通して撮影者の眼に届くという仕組みだ。安価なエントリー機ではペンタプリズムの代わりにペンタミラーが使われることも多い。
実際の一眼レフは光路が複雑に折れ曲がっているので、もっとわかりやすくするために下の図のように引き伸ばしたと考えよう。
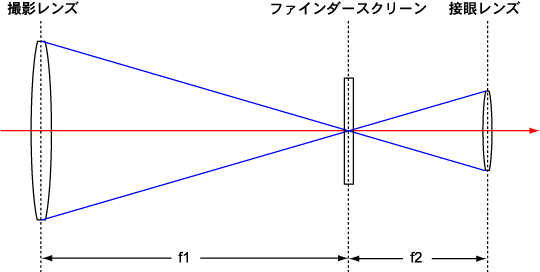
こうして考えると何のことはない、一眼レフのファインダーも望遠鏡や双眼鏡とまったく同じ構造なのである。撮影レンズの焦点距離の位置にファインダースクリーンが置かれ(望遠鏡や双眼鏡にはないが)、さらにその像を接眼レンズで拡大して観察するという構造になっている。ここで撮影レンズの焦点距離をf1、接眼レンズの焦点距離をf2とすると、倍率はf1をf2で割ったものとなる。つまり、
倍率 = f1 / f2
である。これは望遠鏡の場合でも同じで、たとえば天体望遠鏡では対物レンズ(カメラで言う撮影レンズ)の焦点距離が1000mm前後のものが多いが、その場合、接眼レンズの焦点距離が8mmであれば、倍率は1000mm / 8mm = 125倍ということになる。ただし、天体望遠鏡を覗いたことがある人ならわかるだろうが、あれは上下左右が逆さまになって見える。像が動く方向も逆だから、操作には若干の慣れを必要とするが、もともと宇宙には上も下もないのだから実用上はそれで問題はない。しかし地上の風景を写すカメラの場合はそういうわけには行かないので、ペンタプリズムを使って光を複雑に折り曲げ、反転させる必要が出てくる。とりあえずここでは、撮影レンズの焦点距離f1が同じなら、接眼レンズの焦点距離f2が短いほどファインダー倍率は高くなると覚えておこう。
一眼レフカメラの場合、レンズは交換可能だから、f1が変われば当然ファインダー倍率も変わってしまう。そこでカタログスペックを表記する場合には基準が必要だ。これはフィルム時代からの慣習で、135判カメラの場合は50mmレンズを装着した場合の倍率で表記することになっている。50mmレンズというのは要するに標準レンズのことだが、実はここにインチキの種が潜んでいる。
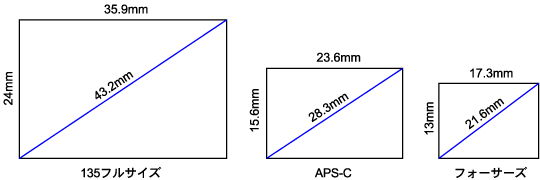
上の図は各フォーマットの画面サイズと対角線の長さを求めたものだ。言うまでもなく、対角線長は画面サイズがわかればピタゴラスの定理によって計算可能だ。厳密に言うと、一眼レフカメラのファインダー倍率はそのフォーマットにおける「標準レンズ」を装着した場合で評価しなければならない。そして標準レンズとは画面の対角線長に等しい焦点距離を持つレンズのこととされている。したがって135判の場合、厳密には43.2mmを標準レンズとすべきだが、なぜかライカ社が50mmを標準レンズとしたために以後そうなったという経緯がある。しかしまあそのくらいは誤差と思って、少なくとも135判においては50mmレンズを装着した場合の倍率を表記するということに決めてしまえばそれで問題はない。ちなみに倍率というのは肉眼で見た場合の大きさに対する像の大きさの比率だから、両目を開けてファインダーを覗いてみるとよくわかる。たとえばファインダー倍率が0.7倍のカメラに50mmレンズを装着して両目で見比べてみると、ファインダーの像は肉眼で見るより少し小さく見えるはずだ。0.7倍というのは焦点距離が50mmの場合だから、当然望遠になるほど倍率は高くなる。もしズームレンズを持っていれば、焦点距離を70mmくらいにセットすると、ほぼ肉眼で見た大きさと同じになることもわかるだろう。
以上、世の中がほとんど135判であったフィルム時代はそれで問題はなかったのだが、これがデジタルカメラになると話が違ってくる。なぜなら、デジタルカメラの画面サイズというのはフォーマットによってまちまちだからである。画面サイズが違えば当然対角線長も異なり、したがって「標準レンズ」の定義自体が変わってくる。上の図からわかるように、APS-Cなら28.3mm、フォーサーズなら21.6mmを標準レンズとして倍率を評価しなければならない。しかし現実にはどんなフォーマットであろうとフィルム時代の慣習にしたがって50mmレンズを装着した場合の倍率が表記されている。ここがとんでもないインチキなのだ。135フルサイズの場合、50mmに対する43.2mmはまあ誤差の範囲と思っても差し支えないが、まさか28.3mmや21.6mmが「誤差」と言えるはずがない。よく知っているように50mmレンズというのはAPS-Cでは75mm相当になり、フォーサーズでは100mm相当の中望遠レンズになってしまう。それで倍率が0.9倍だとか言っているのだから、まったくメチャクチャな話である。これは明らかに業界ぐるみの恣意的な申し合わせと言えるだろう。
では、カタログスペックを「正しく」読むにはどうすればよいか? それは簡単な話で、すべてフルサイズ基準に換算してしまえばよいのである。上の図から135フルサイズに対する対角線長の比率を求めると、
APS-C: 43.2mm / 28.3mm = 1.53
フォーサーズ: 43.2mm / 21.6mm = 2.00
となる。これは要するに135判換算の焦点距離を求める際の係数と同じだ。どんなフォーマットであろうとカタログスペックにはすべて50mmレンズを装着した場合の倍率が記載されているから、それを上の係数で割ってやればフルサイズ基準での倍率が求められる。いくつかの機種について、実際にカタログから拾ってみると次のようになった。
ニコンD600: 0.7倍 → そのまま
ニコンD7000: 0.94倍 → 0.61倍
ニコンD5100: 0.78倍 → 0.51倍
オリンパスE-5: 1.15倍 → 0.58倍
オリンパスE-620: 0.96倍 → 0.48倍
カタログスペックだけ見るとフォーサーズがずいぶん立派に見えるが、それは100mm相当の話だから大きなインチキだ。こうやって「真の」倍率を比較すると、フォーサーズのファインダーがいかに小さいかがよくわかる。高級機のE-5であっても0.6倍に満たないのだ。E-620に至っては、OM-4Tiと比べると2倍近く違うのもよくわかる。ファインダーの小ささはフォーサーズの宿命としか言えないのだ。
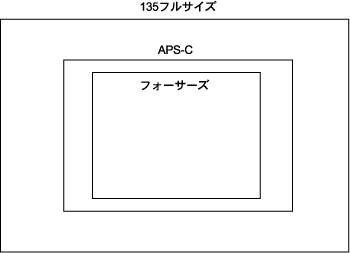
このことは、上の図のように画面サイズを比較してみると容易に理解できる。これは実際の画面サイズと同じ比率になっているが、視野の大きさはフォーマットによってこれほど大きく異なる。背面液晶やEVFの場合は必ず画面いっぱいに拡大されるから、フォーマットによる差というものはあり得ないのだが、光学ファインダーの場合は物理的に周囲をマスクしているのと等価なので、ファインダースクリーンを見る距離が同じなら画面サイズが小さいほどファインダーの視野角(つまり見た目の大きさ)は狭くなる。では、ファインダーの視野角を大きくするためには、見る距離をできるだけファインダースクリーンに近づければよいということになる。つまり接眼レンズの焦点距離f2をできるだけ短くすればよいのだ。
実際に接眼レンズの焦点距離がどのくらいなのかと言うと、それは公表されているわけではない。しかしファインダー倍率がわかれば逆算で求めることはできる。つまり、
f2 = f1 / 倍率
であるから、f1と倍率の両方がわかれば計算可能である。ファインダー倍率は50mmレンズを装着した場合の数値で表されるから、たとえばニコンD600の場合、倍率が0.7倍だから接眼レンズの焦点距離は50mm / 0.7 = 71.4mmとなる。一方、オリンパスE-5の場合は倍率が1.15倍だから、接眼レンズの焦点距離は50mm / 1.15 = 48.9mmとなる。はじめに述べたように、一眼レフというのはファインダースクリーンに映る倒立像を正立像に戻すために、ペンタプリズムで複雑に光路を折り曲げる必要がある。そのために接眼レンズの焦点距離を短くするといっても自ずと限界が存在する。画面サイズが小さくなってもペンタプリズムはそんなに小さくすることができないから、最低でも50mm前後を必要としてしまうのである。もしフォーサーズでも接眼レンズの焦点距離をフルサイズの半分にすることができれば、理論的にはフルサイズと同じファインダー倍率を確保できることになるが、それは物理的に無理なのだ。フルサイズとフォーサーズではせいぜい上で求めたくらいの差にしかならないのだ。
ファインダー倍率を少しでも大きくしたい場合、一つだけ方法がある。それはペンタミラーではなくペンタプリズムを使うことだ。これらはどちらも機能的にはまったく同じだが、中身が中空かガラスで満たされているかの違いがある。その根本的な違いは屈折率にある。一般に真空中での屈折率を1とすれば、媒質中での屈折率はそれよりも大きくなる。たとえば水の屈折率は1.33である。そして光学的な距離は屈折率に反比例するという性質がある。つまり物理的な距離が同じであっても、屈折率が高いほど光学的な距離が短くなるのだ。たとえば、水中では25mプールの反対側の壁が実際より近くに見えたり、浅いと思っていた海の底が意外と深かったりするのもまったく同じ原理だ。ガラスの屈折率というのはもっと高くて、材質によって異なるが概ね1.43~1.73程度である。だから中空のペンタミラーをガラスのペンタプリズムに置き換えるだけで光学的な距離を短くすることができ、その分接眼レンズの焦点距離を短くすることが可能なのだ。つまりファインダースクリーンをより「近くから」覗くのと同じ効果になる。当然ペンタミラーよりペンタプリズムの方が高価なので、エントリー機にはペンタミラーが採用され、中級機以上にはペンタプリズムが採用されているのもそういう理由による。もちろんD600もE-5も高級機だからどちらもペンタプリズムを採用しているが、フォーサーズでは目一杯がんばってもせいぜいその程度ということなのだ。