ネタがないのでしょーもない実験をしてみた。もともとこれをやろうと思ったのは、デジタルカメラの解像度に関するある疑問からである。よくレビューサイトなどでレンズの解像度についてLW/PH(Line Width per Picture Height)という単位で数値的に表現されているのだが、どう考えても腑に落ちない。というのは、サンプリング定理によって解像度は短辺方向の画素数の半分以上にはなり得ないからである。たとえば4000×3000の1200万画素なら短辺方向は3000ピクセルだから、その半分の1500本が解像できる線の本数の上限となる。それは次のようにして考えれば誰にでも容易に理解できるだろう。

この画像は1ピクセルおきに白と黒の縦線を交互に並べたものだ。横幅は512ピクセルあるので、白黒の縦縞はちょうどその半分の256本ある。ここでは画面の都合で縦横入れ替えたけれども、横幅を高さと考えれば同じことだ。つまり画像の高さあたり256本が解像度の限界となる。1ピクセルはこれ以上分割できないのだから、これ以上の本数はどうやっても表現できないことは誰にでもわかるだろう。この解像限界となる空間周波数のことをナイキスト周波数と呼んでいるが、それは一辺の画素数の半分に等しい。これがいわゆるサンプリング定理だ。
ところがレビューサイトの評価結果ではたびたびナイキスト周波数を上回る解像度が出てくる。たとえば4000×3000のセンサーの場合、そこそこ良いレンズならば2000~2300LW/PH程度の数値を示している。短辺方向のナイキスト周波数は1500本だから、これはどう考えても矛盾しているのではないか? 絶対に2000本以上解像できることはあり得ない。LW/PHの定義そのものを勘違いしているのか? 疑問はそこから始まったのである。そしてモアレの再現実験へと発展していく。
まず画像をデジタル化する方法についておさらいしてみる。実は画像も音とまったく同じだから、CDなどと原理的には同じものである。要するに一定の間隔ごとにデータのサンプリングを行い、それを数値化するだけのことである。ただ画像は音と違って2次元なので少し複雑になるが、上に挙げたような縦縞模様で考えれば横方向だけを考えればよいので、1次元の問題に帰着できる。そしてこの縦縞模様を作り出すために、音と同じく正弦波の波形を用いる。これは光の明暗を表していると考える。
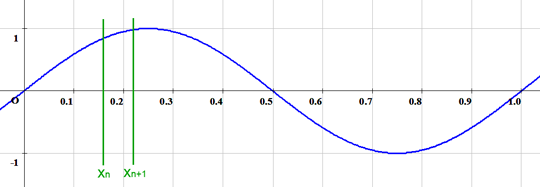
正弦波とはよく知られているようにsin関数のことである。横軸は画像の横方向に対応するものとし、x=0は左端、x=1は右端に対応するものとする。そして縦軸は光の強さを表す。sin関数は-1から1の値をとるから、-1が最も暗い黒に対応し、1が最も明るい白に対応する。0は中間のグレーだ。ただしデジタル画像ではモノクロの輝度は8bitすなわち0~255の数値で表すから、-1~1の範囲を0~255に対応するように引き伸ばし、黒から白まであらゆる明るさを表現できるようにする。これは便宜上のことで、本質とは関係ない。
上のグラフを数式で表すと下のような関数になる。ここでfは空間周波数を表すものとし、上のグラフではf=1としている。sin関数は位相が2π回ると一周して元に戻るので、f=1のとき、xが0から1まで変化する間にちょうど1回転する。つまり画像の左端から右端に向かって明暗の波を1回繰り返し、白黒のパターンが1回現れる。これが空間周波数1の状態だ。
![]()
上の式はxが連続量、つまりアナログの場合だが、これをデジタル化することを考えよう。まず横軸をN等分して、それぞれ左からx0,x1,x2,・・・,xn,xn+1,・・・と名付けるものとする。つまりxnは次のようになる。
![]()
nは0からN-1まで変化し、n=0は画像の左端、n=N-1は画像の右端に対応する。nが0からN-1まで動く間に、xnは0から1まで動くことがわかるだろう(厳密に言うと1の手前まで)。ここでは横幅が512ピクセルの場合を考えているので、N=512とする。つまり分割の幅は1/N = 1/512だから、nが1つ進むごとにxnは1/512ずつ増える。これらのxnが1つの画素に対応すると考える。
そしてこのN分割されたxnのそれぞれについて対応するyの値を求め、それを数値に置き換える。これがデジタル化だ。xnに対応するynを式で表すと次のようになる。
これが離散化されたsin関数である。

この画像はf=1のとき、上の式から画像を生成したものだ。左から白・黒のパターンが1回現れている。sin関数のグラフと比較してみるとよくわかるだろう。もちろん白黒にはっきり分かれるわけではなく、滑らかに変化しているから中間の明るさも存在する。

同様にf=2とすると、周期が半分になるため、白黒のパターンが2回ずつ現れる。これが空間周波数2の状態だ。
ところで空間周波数が比較的小さい間はこれで問題なかったのだが、空間周波数がもっと高くなるとおかしな問題が起こる。それはデジタル化を行う際に、隣接する画素、すなわちxnとxn+1の間のどの場所をとるかでyの値がまったく変わってしまうという問題である。f=1のグラフのように分割の幅に比べてyの変化がゆるやかであれば、xnにおける値をデジタル化しても問題はなかった(あるいはxnとxn+1の中点を取ってもよい)。ところが空間周波数をもっと上げてみるとどうなるだろうか?
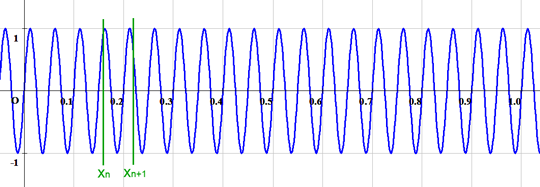
ここまで細かくなると、xnとxn+1の間でyの値が大きく変化してしまうため、この間のどこでデジタル化するかによって結果がまったく異なってしまうということがわかるだろう。これは明らかにおかしい。現実のデジタルカメラに置き換えてみるとよくわかる。撮像センサーは縦横それぞれに数千個の画素に分割されたものだが、それでも1つ1つの画素は有限な面積を持っている。実際には数ミクロン四方といったレベルだが、それでも光の波長に比べれば十分大きい。すると1つの画素の中に明るさが異なる部分が混在しているはずである。上のグラフはそのことを表しているのだ。つまり様々な明るさがミックスされている中でどれを取るかによって結果がまったく異なってしまう。現実のデジタルカメラをシミュレーションするならば、このことは絶対に考慮しなければならない。実際、撮像センサーでは1つ1つの画素ごとにマイクロレンズというものが付いていて、その面積で受けた光を1点に集める構造になっている。とすると、デジタルデータとして出力されるものは、1つの画素で受けたあらゆる光の明るさの総和(もしくは平均)になっていると考えるのが自然だろう。上のグラフで言えば、区間xnとxn+1の間における平均値が実際にセンサーから出力されるデータだと考えられる。するとこれはy(x)をxnからxn+1の間で積分し、区間の幅1/Nで割ったものに等しい。
![]()
この定積分は解析的に求めることができ、離散化されたynとしてはこの式を採用するものとする。これが現実の撮像センサーに最も近いと考えられるからだ。別にこの式の意味を理解する必要はない。論理的な根拠を示すために書いただけで、わかる人だけ考えればよい。大事なのは画像としてどのようなパターンが現れるかだ。
次に上の式ynを用いて空間周波数f=10, f=20, f=40, f=80の場合に画像を生成した結果を示す。それぞれ空間周波数に等しい本数の白黒の線が見えることが確認できるだろう。




そしてf=256、すなわちパターンのピッチと画素ピッチが完全に一致したときはどうなるか?

これが最初に示した白黒の線が1ピクセルおきに並んでいる状態だ。すなわち最大解像度に対応するナイキスト周波数の場合である。このとき正弦波の山と谷がピッタリ画素ピッチに一致している。ただ拡大してよく見ると完全な白と黒ではなく、グレーになっていることがわかる。これは正弦波の山と谷を平均化してならしたためである。言い換えれば、コントラストが100%ではなく、少し低下した状態と言える。
さて、この実験をやりたかった最大の目的は、ナイキスト周波数付近でどのような現象が起こるかを見たかったからである。そこでf=256を中心に、f=255,254,・・・と減らす方向とf=257,258,・・・と増やす方向でそれぞれ検証してみた。まず減らす方向は次の通り。



おっと、何やら規則性が見えてきたではないか! ぼんやりと暗い縞模様が見えるが、その本数は2本、4本、6本と増えている。つまり一般化すると、(256-f)x2本だけ縞模様が見えるようだ。試しにf=246にしてみると、

やはり20本の縞模様が見えた。今度は逆にf=257から増やしてみる。このときはすでにナイキスト周波数を超えていることに注意。




おや、ナイキスト周波数を境にして同じ現象が対称的に起こっているようだ。これがモアレの正体なのか? しかしちょっと待てよ。ナイキスト周波数以下であればモアレは起こらないはずじゃないのか? それでもモアレみたいな縞模様が見えるということはなぜなんだ? これはモアレじゃないのか?
モアレ(moire)というのはフランス語で、干渉縞を表す用語らしい。どうやら自分が思っていたよりももっと広義の意味に使われているようだ。そうするとこれもモアレの一種には違いないが、どうやら2種類のモアレが存在することがわかってきた。一つはこのナイキスト周波数近辺で生じる縞模様のことだ。これは正確に言うと「唸り」に近いものだろう。f=256のときはパターンのピッチと画素ピッチが完全に一致しているから縞模様は見えないが、もし1ピクセルでもずれるとどうなるか? すると画素をまたぐパターンが必ず出てくる。それが平均化されて微妙な輝度の差となり、縞模様となって見えるのだろう。これはちょうど重なった2枚の網を遠くから眺めたとき、波打った模様が見えるのと同じ現象と考えられる。あれも一種の唸りであり、肉眼でも見えるから実像である。画像をデジタル化するということは、言い換えれば網の目を通してものを見ているのと似ているから同じ現象が起こるのだろう。そしてナイキスト周波数を挟んで対称的に同じ現象が起こるということは、2枚の網の反対側から眺めたのと同じことなのだ。2枚の網のどっち側が手前であろうと唸りが起こることには違いはない。だからこれはナイキスト周波数を超えたことによって起こるデジタル化に特有のモアレではないが、広義のモアレには含まれるのだろう。
では次にf=512、すなわち空間周波数が横方向の画素数と同じ場合を考える。これはナイキスト周波数のちょうど2倍に相当する。

すると一様なグレーになって縞模様は1本も見えない。これはちょうど1画素の中に正弦波の山と谷が両方入った状態であり、平均するとゼロになってしまうため、当たり前の結果だ。次にf=511, 510と一つずつ減らしてみよう。


するとやはり一様なグレーになって縞模様は見えない。本当はそれぞれ1本、2本ずつ見えているはずなのだが、コントラストがほとんどないので人間の目には識別できないということだ。次にf=502まで減らしてみる。

今度はうっすらと10本の縞模様が見えた。これはもちろん実像ではない。デジタル化によって生じたいわゆるエイリアスノイズである。ナイキスト周波数を境にしてちょうど裏返しの関係になっており、f=512から数えて逆に戻るごとに本数が増えていく。以下、それを確かめてみよう。



確かに(512-f)本の縞模様が見えている。これはそれぞれf=10, 20, 40, 80の場合に相似である。ただし、それよりもコントラストが低くなっていることがわかる。これは白黒のパターンの幅が画素ピッチより狭くなったため、平均化されてグレーに近付いているからである。もし平均化をやらなければこういう結果にはならない。
そしてこのナイキスト周波数の2倍付近で生じる縞模様こそが本当の意味でデジタル化に特有のモアレなのだ。それはナイキスト周波数を境にして対称的に現れる。言い換えればナイキスト周波数以上の領域はそれ以下の領域の鏡像になっており、意味を持たない。決して256本以上の線が解像できるわけではないのだ。
ではここでデジタルカメラでよく問題にされるモアレについて考えてみよう。モアレには輝度モアレと色モアレの2つが存在することが知られているが、ここで考えたのは輝度モアレの方。通常のベイヤー配列センサーではいわゆるRGGBの4画素を1組にして色を作り出しているから、色の解像度としては画素数の1/4程度しかないと考えられる。しかしそれぞれの画素は光の強さ自体は感じることができるから、モノクロの輝度情報にしてしまえばおおよそ1ピクセル単位で解像力を持っていると考えられる。だから輝度に関しては解像度は画素数とほぼイコールであり、ナイキスト周波数は一辺の画素数の半分程度と考えて良い。しかし色情報に関しては画素数の1/4程度の解像度しかないから、色情報に関するナイキスト周波数は輝度情報のそれよりもかなり低い。したがって色モアレの方がより起こりやすいと言える。
通常、デジタルカメラにローパスフィルターが用いられる理由は色モアレを防ぐことが目的である。ローパスフィルターはある空間周波数より低い成分だけを通し、それより高い周波数成分をカットする働きをする。そして色モアレが起こる空間周波数は輝度モアレが起こる周波数よりもかなり低いから、色モアレに合わせてチューニングすると解像度がかなり損なわれてしまう。だからローパスフィルターが悪者扱いされるわけだが、ベイヤー配列の構造上、色モアレを防ぐためにはやむを得ないのだ。一方、輝度モアレが起こる空間周波数は、上で確かめたようにナイキスト周波数付近より高い領域であるから、色モアレに合わせてチューニングされたローパスフィルターを持つデジタルカメラでは高周波成分が十分カットされており、原理的に輝度モアレは起こり得ないと考えられるだろう。特に狭い意味でのモアレ(エイリアスノイズ)はナイキスト周波数の2倍に近い領域で起こるから、昔の600万画素時代ならともかく、現代の高画素化されたセンサーではまず起こり得ないと考えられるだろう。レンズの解像度の方がそこまで高くないので、レンズ自体がローパスフィルターの役割を果たしているからだ。そしてナイキスト周波数近辺で起こる「唸り」の方はローパスフィルターの効きが弱いともしかすると起こるかもしれない。一方、ローパスフィルターレスのカメラでは色モアレ、輝度モアレの両方とも起こる可能性がある。やはり輝度モアレの方がより起こりにくいが、もし起こったとすればそれはエイリアスノイズではなく「唸り」である可能性が高い。ナイキスト周波数の2倍近くで起こるエイリアスノイズが発生するためにはレンズの解像度が相当高くないと無理なはずだ。
そして初めの問題に戻るが、ナイキスト周波数を超える解像度があり得るのか?といえば、上で確かめたようにやはりあり得ない。ナイキスト周波数を超えて現れる模様はすべてエイリアスノイズであり、実像ではない。しかも空間周波数が高くなるほど平均化されてコントラストが下がっていく。だから短辺の画素数と同じだけの本数が解像できるということはあり得ないのだ。
するとLW/PHの定義そのものを勘違いしていたと考えるのが自然である。実は解像度を表す指標にはもう一つLP/mm(Line Pairs per mm)というのがある。こちらはMTFの評価でよく用いられるものだが、文字通りミリメートル当たり何本の白黒の線のペアを表現できるかということを表している。これは撮像面における物理的な解像度のことだからわかりやすい。それに対してLW/PHというのは、もともとテレビ画面の解像度を表現するために考案されたものだ。つまり画面の短辺方向に何本の線を引けるかということを表している。たとえば現在のハイビジョンテレビは短辺1080ピクセルだから、1080LW/PHということになる。これはLP/mmのように白黒の線のペアを何本識別できるかではなく、単に異なる色として分離できるかを表しているらしい。だから基本的に画面のピクセル数とイコールなのだ。そんなの今どきの液晶テレビじゃ当たり前のように思えるが、たぶんこれはブラウン管時代の名残なのだろう。ブラウン管はアナログだから画面に何本線が引けるかは一定じゃない。線を細くするほどぼやけてくる。確かにそれなら意味はわかる。
そうするとレンズの解像度をLW/PHで表すのってやっぱり変だと思うのだ。レンズの純粋な解像度を比較するなら、物理単位であるLP/mmで表す方が適当だろう。それに換算するためにはLW/PHをセンサーの短辺方向のサイズ(mm)で割り、さらに2で割ればよい。2で割る理由は白黒の線のペアで考えるためだ。これでやっと理解できた。とにかくよくわからんことは知ったかぶりをするのが一番恥ずかしい。しょーもない実験をしてでも自分が納得できるまで確認すべし。

